Question

Show work and explain with formulas.

10. Find the sum (see picture).

11. Find the sum of the geometric series: a_2 = -36, a_5 = 972, n = 7

12. Find the first term: S_n = 315, a_n = 5, r = 1/2, n = 6​

Answer 1

`\large\boxed{10.\ \sum\limits_(n=1)^(9)5(2)^(n-1)=2,555}`

`\large\boxed{11.\ S_7=6,564}`

`\large\boxed{12. a_1=160}`

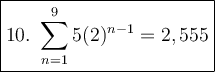
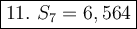
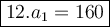
Explanation:

10.

The formula of a sum of terms of a geometric sequence:

`S_n=(a_1(1-r^n))/(1-r)`

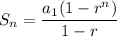
We have:

`\sum\limits_(n=1)^(9)5(2)^(n-1)`

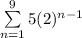
Therefore:

`a_n=5(2)^(n-1)\to a_1=5(2)^(1-1)=5(2)^0=5(1)=5`

`r=(a_(n+1))/(a_n)\\\\a_(n+1)=5(2)^(n+1-1)=5(2)^n\\\\r=(5(2)^n)/(5(2)^(n-1))=(2^n)/(2^(n-1))\qquad\text{use}\ (a^n)/(a^m)=a^(n-m)\\\\r=2^(n-(n-1))=2^(n-n+1)=2^1=2`

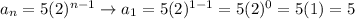
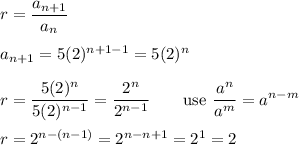
Substitute a₁ = 5, r = 2 and n = 9:

`S_9=(5(1-2^9))/(1-2)=(5(1-512))/(-1)=-5(-511)=2,555`

==========================================

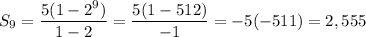
11.

We have

`a_2=-36,\ a_5=972,\ n=7`

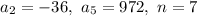
We know:

`a_n=a_1r^(n-1)`

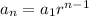
Therefore

`a_2=a_1r^(2-1)=a_1r^1=a_1r\\\\a_5=a_1r^(5-1)=a_1r^4\\\\(a_5)/(a_2)=(a_1r^4)/(a_1r)=r^(4-1)=r^3`

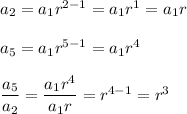
Substitute:

`r^3=(972)/(-36)\\\\r^3=-27\to r=\sqrt[3]{-27}\\\\r=-3`

Calculate the first term:

`a_2=a_1r\to a_1=(a_2)/(r)\\\\a_1=(-36)/(-3)=12`

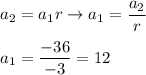
Put a₁ = 12, r = -3 and n = 7 to the formula of a sum:

`S_7=(12(1-(-3)^7))/(1-(-3))=(12(1-(-2187)))/(1+3)=(12(1+2187))/(4)=3(2188)\\\\S_7=6564`

==========================================

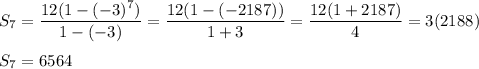
12.

We have

`n=6,\ S_n=315\to S_6=315,\ a_n=5\to a_6=5,\ r=(1)/(2)`

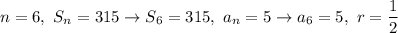
We know:

`a_n=a_1r^(n-1)\to a_6=a_1r^(6-1)=a_1r^5`

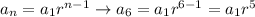
Substitute:

`5=a_1\left((1)/(2)\right)^5\\\\5=(1)/(32)a_1\qquad\text{multiply both sides by 32}\\\\160=a_1\to a_1=160`

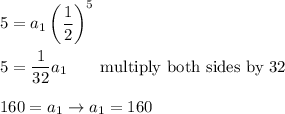
Check for the given sum:

Substitute a₁ = 160, r = 1/2 and n = 6:

`S_6=(160\left(1-\left((1)/(2)\right)^6\right))/(1-(1)/(2))=(160\left(1-(1)/(64)\right))/((1)/(2))=160\left((64)/(64)-(1)/(64)\right)\left((2)/(1)\right)\\\\=160\left((63)/(64)\right)(2)=(2.5)(63)(2)=315`

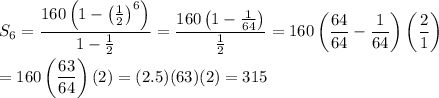
CORRECT :)