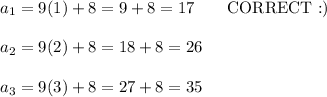Answer:
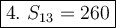
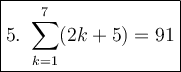
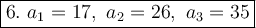
Explanation:
4.
We have:

These are the terms of the arithmetic sequence.
We know:
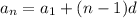
Therefore
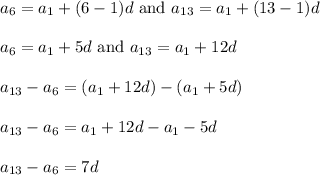
Substitute a₆ = 18 and a₁₃ = 32:
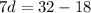
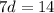 divide both sides by 7
divide both sides by 7
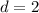
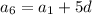

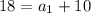 subtract 10 from both sides
subtract 10 from both sides
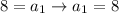
The formula of a sum of terms of an arithmetic sequence:
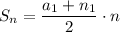
Substitute a₁ = 8, a₁₃ = 32 and n = 13:
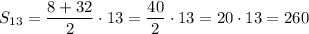
===========================================
5.
We have
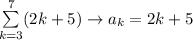
Calculate

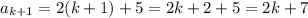
Calculate the difference:
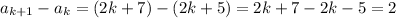
It's the arithmetic sequence with first term
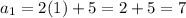
and common difference d = 2.
The formula of a sum of terms of an arithmetic sequence:
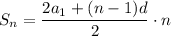
Substitute n = 7, a₁ = 7 and d = 2:
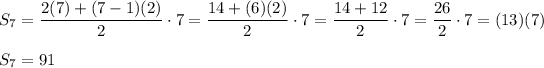
===========================================
6.
We have:

The formula for the n-th term of an arithmetic sequence:
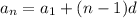
The formula of the sum of terms of an arithmetic sequence:
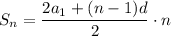
Substitute:
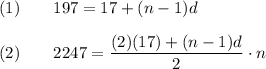
Convert the first equation:
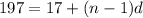 subtract 17 from both sides
subtract 17 from both sides
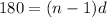 Substitute it to the second equation:
Substitute it to the second equation:

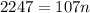 divde both sides by 107
divde both sides by 107

Put the value of n to the equation (n - 1)d = 180:
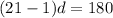
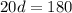 divide both sides by 20
divide both sides by 20
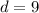
Therefore we have the explicit formula for the nth term of an arithmetic sequence:
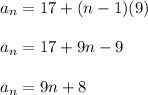
Put n = 1, n = 2 and n = 3: