Question

Which of the following functions shows the quadratic parent function, f(x)= x^2, shifted left?

A. G(x)= x^2+18
B. G(x)= (x-3)^2
C. G(x)= (x+8)^2
D. G(x)= x^2-7

Answer 1

The answer is C) because you are moving left 8 units. In the inside of the parenthesis it says +8 however its counterintuitive, so the function is actually moving left. You can check on desmos.com a website for graphing functions.

Answer 2

`G(x)= (x+8)^2`

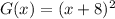
Explanation:

Parent function:
`f(x)= x^2`

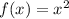
Rule : f(x)→f(x+b)

The graph shifts left by b units

So,
`f(x)= x^2`

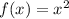
Now shifting this graph left by b units .

`f(x+b)= (x+b)^2`

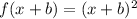
So, the shifted graph is
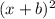`(x+b)^2` --A

On comparing all the given options with A

We can say that Option C is correct.

`G(x)= (x+8)^2`

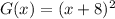
The parent graph shifted left by 8 units.

Thus
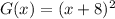`G(x)= (x+8)^2` hows the quadratic parent function,
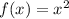`f(x)= x^2`shifted left