Answer:
Part a)
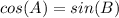
Part b)
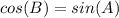
Part c)
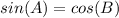
Part d)
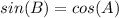
Explanation:
we know that
In the right triangle ABC of the figure
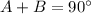 ----> by complementary angles
----> by complementary angles
so
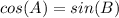
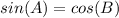
Part a) Cos(A)
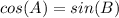
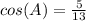
The value of cosine of angle A is the ratio between the adjacent side angle A to the hypotenuse
Part b) Cos(B)
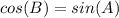
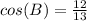
The value of cosine of angle B is the ratio between the adjacent side angle B to the hypotenuse
Part c) Sin(A)
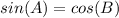
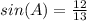
The value of sine of angle A is the ratio between the opposite side angle A to the hypotenuse
Part d) Sin(B)
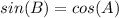
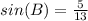
The value of sine of angle B is the ratio between the opposite side angle B to the hypotenuse