Answer:
The measure of the
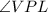 is
is
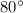
Explanation:
We know that the measure of the inner angle is the semi-sum of the arcs comprising it and its opposite.
Now, Let
x is the measure of arc IV
and y is the measure of arc PK, then
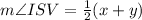
Substituting the given values, we get
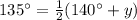
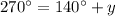
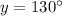
Thus, The measure of arc PK is
 .
.
Also, we know that the inscribed angle measures half that of the arc comprising , thus
Let
z is the measure of arc VK
and y is the measure of arc PK, then
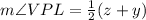
Substituting the values, we get
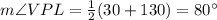
Hence, the measure of the
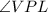 is
is
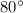 .
.