Answer:
The statements which are true regarding the system of equations is:
- The y-intercepts are different.
- The system has no solution.
Explanation:
The equation of a line in slope-intercept form is given by:
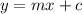
where m is the slope of the line and c is the y-intercept of a line.
The first equation is:
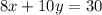
i.e. on converting this equation to slope-intercept form we get:
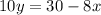
i.e.
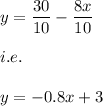
The slope of first line is: -0.8
and y-intercept is: 3
and the second equation is:

i.e. on converting this equation to slope-intercept form we get:
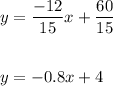
The slope of second line is: -0.8
and y-intercept is: 4
Since, the slope of both the line are equal (i.e. -0.8)
This means that the two lines are parallel and hence they will never coincide.
Hence, the system has no solution.
Also, the y-intercepts are different.