Question

What are the angles of △ABC with side lengths a=27, b=11, and c=19?

Select the correct answer below:

A=126.2∘, B=19.2∘, and C=34.6∘

A=126.2∘, B=21.2∘, and C=32.6∘

A=126.2∘, B=17.2∘, and C=36.6∘

A=123.2∘, B=19.2∘, and C=37.6∘

Answer 1

The first one is correct

A=126.2∘, B=19.2∘, and C=34.6∘

Sorry that the names for the angles are mixed up and its in german but they are correct

Answer 2

The correct answer option is A) A=126.2°, B=19.2°, and C=34.6°.

Explanation:

Using cosine rule to find angle A:

`a^2=b^2+c^2-2bc cos A`

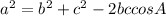
Substituting the given values in the formula to get:

`27^2=11^2+19^2-2(11)(19) cos A`

`729-482=-418cos A`

`A=cos'(-0.590)`

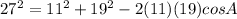
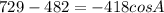
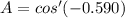
A = 126.2°

Now that we have found one angle, we can use sine rule to find the other two angles.

`(SinA)/(a) =(Sin B)/(b)`

`(Sin 126.2)/(27) =(Sin B)/(11)`

`B=sin'(0.328)`

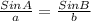
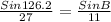
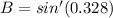
B = 19.2°

`(SinB)/(b) =(Sin C)/(c)`

`(Sin 19.2)/(11) =(Sin C)/(19)`

`C=sin'(0.567)`

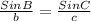
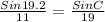
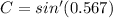
C = 34.6°

Therefore, the correct answer option is A) A=126.2°, B=19.2°, and C=34.6°.