Question

Write the absolute value inequality in the form Ix−bIc that has the solution set x≤−9 or x≥−5.

Answer 1

`x \le -9 \ \text{ or } x \ge -5`

`x \le -7 - 2 \ \text{ or } x \ge -7 + 2`

`x+7 \le -7 - 2+7 \ \text{ or } x+7 \ge -7 + 2+7`

`x+7 \le -2 \ \text{ or } x+7 \ge 2`

`|x+7| \ge 2`

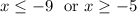
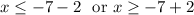
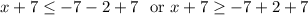
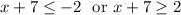
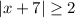
So the final answer is
`|x+7| \ge 2`

---------------------------

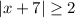
side notes:

• The -7 in step 2 is the midpoint of -9 and -5. You add up -9 and -5 to get -14, then divide by 2 to get -7.
• x+7 is the same as x-(-7)
• For the last step I used the rule that if |x| > k then x < -k or x > k for some positive number k

Answer 2

`\large\boxed\geq2`

Explanation:

Look at the picture.

`|x-a|\geq b\\\\a=(-9+(-5))/(2)=(-14)/(2)=-7\\\\b=-9-(-7)=-9+7=-2\\b=-5-(-7)=-5+7=2\\\\|x-(-7)|\geq2\\\\|x+7|\geq2\\\\Check:\\\\|x+7|\geq2\iff x+7\geq2\ \vee\ x+7\leq-2\qquad\text{subtract 7 from both sides}\\\\x+7-7\geq2-7\ \vee\ x+7-7\leq-2-7\\\\x\geq-5\ \vee\ x\leq-9\qquad CORRECT\ :)`