Answer:
Option D)
Explanation:
If the graph of the function
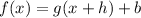 represents the transformations made to the graph of
represents the transformations made to the graph of
 then, by definition:
then, by definition:
If
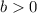 the graph moves vertically b units up
the graph moves vertically b units up
If
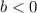 the graph moves vertically b units down
the graph moves vertically b units down
If
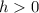 the graph moves horizontally h units to the left
the graph moves horizontally h units to the left
If
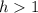 the graph moves horizontally h units to the rigth
the graph moves horizontally h units to the rigth
In this problem we have the function
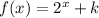 and our parent function is
and our parent function is
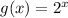
therefore it is true that
 and
and
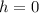
Then "The graph of f(x) is shifted k units below the graph of g(x)".
The answer is Option D)
_________________________________________________
Note:
If the function are:

Then
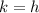 and
and
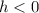 . This means that the function f(x) shifts k units to the right of the function g(x)
. This means that the function f(x) shifts k units to the right of the function g(x)
And the answer would be the option B)