Question

Alex the electrician needs 34 yards of electrical wire to complete his job. He has a coil of wiring in his workshop. The coiled wire is 18 inches in diameter and is made up of 21 circles of wire. Will this coil be enough to complete the job? Let Pi be 3.14.

Answer 1

Answer: This coil will not be enough to complete the job.

Explanation:

The circumference of the coil of wiring can be calculated with:

`C=2\pi r`

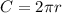
Where r is the radius and
`\pi=3.14`

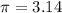
The radius can be calculated by dividing the diameter by 2. Then:

`r=(18in)/(2)\\\\r=9in`

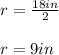
Convert 9 inches to yards (1 yard=36 inches):

`(9in)((1yd)/(36in))=0.25yd`

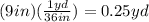
Substitute this radius into the formula:

`C=2(3.14)(0.25yd)\\C=1.57yd`

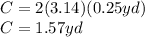
Since there are 21 circles of wire, you need to multiply
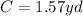`C=1.57yd` by 21:

`C_T=(1.57yd)(21)=32.97yd`

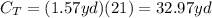
The coil has 32.97 yards of wire and Alex needs 34 yards, therefore, this coil will not be enough to complete the job.