Answer:

Explanation:
The exponential growth formula is

Where
A is the main coefficient and represents the initial population.
e is the base
k is the growth rate
t is time in years.
Let's call t = 0 to the initial year 1993.
At t = 0 the population was 94 millions
Therefore we know that:
 millions
millions
After t = 6 years, in 1996, the population was 99 millions.
Then
 million.
million.
Now we use this data to find the variables a, and k.
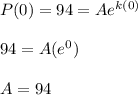 .
.
Then:
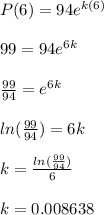
Finally the function is:
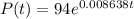
In the year 2005:
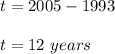
So the population after t=12 years is:

