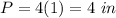A square is inscribed in an isosceles right triangle. Length of the leg equals to 2 in. as shown on the figure. Find the perimeter of the square.

Question

asked Dec 22, 2020 174 views

1 Answer

Piotr Jurkiewicz · Answer 1 · 2020-12-25T18:03:26+0000

Answer:

The perimeter of the square is
$4\ in$

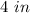
Explanation:

Let

x----> the length side of the square

we know that

In an isosceles right triangle the measures of the internal angles are 45°-90°-45°

so

the horizontal distance is equal to the vertical distance

2=x+x

$x=1\ in$

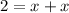
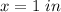
The perimeter of the square is

P=4b

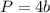
we have

$b=1\ in$

substitute

$P=4(1)=4\ in$