Question

Can you guys help me ?

Answer 1

Your answer would be
`\sqrt[12]{8}^(2)`.

Approaching this problem would be easier by converting the cube root of 8 to 8 to the power of 1/3. Remember that when you take anything to the nth root, it is the same as taking something to the power of 1 / n.

Therefore, the equation becomes
`(x^(1/3) )^{(1)/(4)x }`.

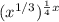Now, to keep simplifying, recall that when you do
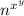`n^(x^y)`, it can become
`n^(x*y)`.

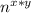This can be applied in this situation. You are taking 8 to the power of 1/3 to the power of 1/4x. Now, you can multiply the two "to the power of's" to get
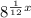`8^{(1)/(12)x }`. Applying the same logic, it becomes
`8^{(1)/(12) *x}  = 8^{(1)/(12) ^x}`.

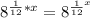Now, all you have to do is use the same logic as used in the very beginning. Raising something to the power of 1/12 can become taking it to the 12th root. So therefore, the equation would be
`\sqrt[12]{8}^(x)`

Good luck!

Answer 2

C the 12th root of (8^x)

Explanation:

This becomes 8 ^ x/4 ^ 1/3

We know that a^b^c = a^ (c*c)

8 ^(x/12)