Question

Which of the following types of symmetry does the graph of the equation r=6sin 5 theta have?

Answer 1

The correct option is 2.

Explanation:

1. Symmetry about the x-axis: If the point (r, θ) lies on the graph, then the point (r, -θ ) or (-r, π - θ ) also lies on the graph.

2. Symmetry about the y-axis: If the point (r, θ ) lies on the graph, then the point (r, π - θ ) or (-r, -θ ) also lies on the graph.

3. Symmetry about the origin: If the point (r, θ ) lies on the graph, then the point (-r, θ ) or (r, π + θ ) also lies on the graph.

The given equation is

`r=6\sin (5\theta)`

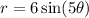
Check the equation by (r, -θ ).

`r=6\sin (5(-\theta))`

`r=-6\sin (5\theta)=-r\\eq r`

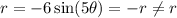
The given equation do not have symmetry about the x-axis or horizontal axis.

Check the equation by (-r, -θ).

`-r=6\sin (5(-\theta))`

`-r=-6\sin (5\theta)`

`-r=-r`

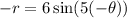
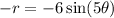
LHS=RHS

The given equation have symmetry about the y-axis or vertical axis.

Check the equation by (-r, θ).

`-r=6\sin (5\theta)`

`-r\\eq r`

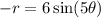
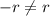
The given equation do not have symmetry about the origin or pole.

Therefore the correct option is 2.

Answer 2

B

Explanation:

Plot the graph of the equation
`r=6\sin 5\theta` on the polar coordinate plane (see attached diagram for details).

A. There is no symmetry about the horizontal axis, because three parts of the graph are above the axis and two parts of the graph are under the axis.

B. There is symmetry about the vertical axis, because if you reflect left (or right) part about the vertical axis it will coincide with the other part.

C. There is no symmetry about the pole (see diagram)

D. This option is false, because option B is true (there is axis of symmetry)