In summary, the polar coordinate pairs that represent the same point as
 when
when
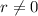 are:
are:
1.

2.
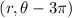
To determine which of the given polar coordinate pairs represents the same point as the point with polar coordinates
 when
when
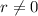 , we can use the following relationships in polar coordinates:
, we can use the following relationships in polar coordinates:
1.
 represents a point with distance
represents a point with distance
 from the origin and an angle of
from the origin and an angle of
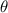 from the positive x-axis.
from the positive x-axis.
Now, let's examine each of the options one by one:
1.

This represents a point with the same distance
 from the origin, but the angle is
from the origin, but the angle is
 , which is the same as
, which is the same as
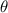 since subtracting
since subtracting
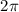 from an angle is the same as not changing the angle at all.
from an angle is the same as not changing the angle at all.
So, this coordinate pair represents the same point:
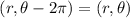 .
.
2.
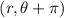
This represents a point with the same distance
 from the origin, but the angle is
from the origin, but the angle is
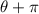 . Adding
. Adding
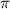 to an angle means rotating the point by
to an angle means rotating the point by
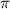 radians in the opposite direction (180 degrees).
radians in the opposite direction (180 degrees).
So, this coordinate pair represents the same point:
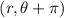 is the opposite direction but the same distance, so it's equivalent to
is the opposite direction but the same distance, so it's equivalent to
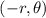 .
.
3.
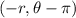
This represents a point with the distance
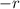 , which doesn't make sense in polar coordinates because distances should be positive. So, this option is not valid.
, which doesn't make sense in polar coordinates because distances should be positive. So, this option is not valid.
4.
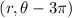
This represents a point with the same distance
 from the origin, but the angle is
from the origin, but the angle is
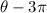 . Subtracting
. Subtracting
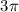 from an angle is the same as subtracting
from an angle is the same as subtracting
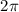 (a full rotation) plus an additional
(a full rotation) plus an additional
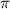 radians, which is equivalent to rotating by
radians, which is equivalent to rotating by
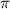 radians in the opposite direction.
radians in the opposite direction.
So, this coordinate pair represents the same point:
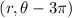 is equivalent to
is equivalent to
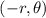 .
.
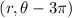
Option 3,
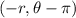 , is not valid as it has a negative distance.
, is not valid as it has a negative distance.