Question

What is an equation of the line that is perpendicular to y+1=-3(x-5) and passes through the point 4,-6

Answer 1

The equation of the perpendicular through the point (4,-6) is
`y + 6 = (1)/(3)( x - 4 )`.

Given the equation of the original line:

y + 1 = -3( x - 5)

Using the point-slope formula, y - y₁ = m( x - x₁ ), the slope of the original line is:

Slope m = -3

The slope of the perpendicular line is a negative reciprocal of the original slope.

The slope of the perpendicular line = 1/3.

Plug the slope m = 1/3 and point (4,-6) into the point-slope form and simplify:

y - y₁ = m( x - x₁ )

`y - (-6) = (1)/(3)( x - 4 ) \\y + 6 = (1)/(3)( x - 4 )`

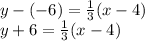
Therefore, the equation of the perpendicular line is
`y + 6 = (1)/(3)( x - 4 )`.

Answer 2

`y=(1)/(3)x-(16)/(3)`

Explanation:

Arranging the given equation in slope-intercept form ( y = mx + b ):

`y+1=-3(x-5)\\y+1=-3x+15\\y=-3x+15-1\\y=-3x+14`

We know that the perpendicular line would have a slope (m) that is negative reciprocal of this (
`(1)/(3)`). Thus we can write the perpendicular line's equation as
`y=(1)/(3)x+b`.

Now putting x = 4 and y = -6 into the equation, we can solve for b:

`y=(1)/(3)x+b\\-6=(1)/(3)(4)+b\\-6=(4)/(3)+b\\b=-6-(4)/(3)\\b=-(16)/(3)`

Thus, the equation of the perpendicular line is
`y=(1)/(3)x-(16)/(3)`