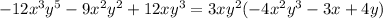Question

Factor the GCF: −12x3y5 − 9x2y2 + 12xy33xy2(−4x2y3 − 3x + 4y)−3xy2(4x2y3 − 3x + 4y)−3(4x3y5 + 3x2y2 − 4xy3)−3xy2(4x2y3 + 3x − 4y)

Answer 1

`3xy^2(-4x^2y^3-3x+4y)`

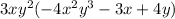
Explanation:

The given expression is

`-12x^3y^5-9x^2y^2+12xy^3`

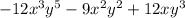
To find the greatest common factor; we find the prime factorization of each term in the expression.

`-12x^3y^5=-2^2*3*x^3* y^5`

`-9x^2y^2=-3^2* x^3 * y^2`

`12xy^3=2^2* 3* x* y^3`

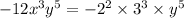
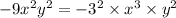
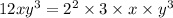
The greatest common factor is the product of the least powers of the common factors.

`GCF=3xy^2`

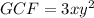
We factor the GCF to obtain;

`-12x^3y^5-9x^2y^2+12xy^3=3xy^2(-4x^2y^3-3x+4y)`