Question

Find the area of shaded region. Round to the nearest tenth.

angle is 100 degrees

r= 8.35 ft

Answer 1

The answer above is wrong ⚠️ caution

Explanation:

The real answer is 192.5

Fill in 192.5

Answer 2

The solution is 192.83 ft²

Explanation:

We need to find out the shaded region of the provided figure

Area of sector calculated as
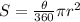`S=(\theta)/(360) \pi r^(2)` and

Area of triangle is calculated as
`A=(1)/(2) r^(2) \sin \theta`

Area of circle is calculated as
`C=\pi r^(2)`

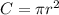
Where r is radius

so,

Area of sector is
`S=(\theta)/(360) \pi r^(2)`

`S=(100)/(360) 3.14 (8.35)^(2)`

`S=(5)/(18) 3.14 (8.35)^(2)`

`S=(5)/(18) 218.92`

`S=60.81`

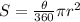
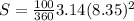
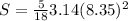
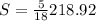
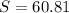
Area of triangle is
`A=(1)/(2) r^(2) \sin \theta`

`A=(1)/(2) (8.35)^(2) \sin 100`

`A=(1)/(2)68.32`

`A=34.16`

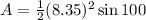
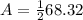
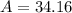
Area of circle is
`C=\pi r^(2)`

`C=3.14 (8.35)^(2)`

`C=3.14 * 69.72`

`C=218.92`

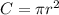
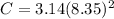
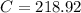
Area of segment = area of sector - area of triangle

= 60.81 - 34.16

= 26.09 ft²

Area of shaded region = area of circle - Area of segment

= 218.92 - 26.09

= 192.83 ft²

Therefore, the solution is 192.83 ft²