Question

S=a1/1-r

help!

this is the formula for a converging infinite series. a1 is the first term and r is the common ratio

Answer 1

4

Explanation:

This is an infinite geometric series. This has a sum of
`(a)/(1-r)`

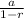
Where

a is the first term, and

r is the common ratio (one term divided by the previous term)

Let's figure out the first 2 terms by plugging in n = 1 first and then n = 2 for the series.

First term:

`3((1)/(4))^(n-1)\\=3((1)/(4))^(1-1)\\=3((1)/(4))^0\\=3(1)\\=3`

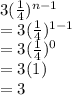
Second term:

`3((1)/(4))^(n-1)\\=3((1)/(4))^(2-1)\\=3((1)/(4))^1\\=3((1)/(4))\\=(3)/(4)`

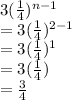
Let's see the common ratio:
`((3)/(4))/(3)\\=(3)/(4)*(1)/(3)\\=(1)/(4)`

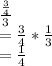
Thus we have a = 3 and r = 1/4. Plugging into the formula of the infinite sum, we get:

`s=(a)/(1-4)=(3)/(1-(1)/(4))=(3)/((3)/(4))=3*(4)/(3)=4`

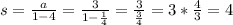
So, the answer is 4