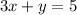Question

If the distance of P x, y from the points A (3, 6) and B −3, 4 are equal, prove that

3x + y = 5

Answer 1

See Below.

Explanation:

We are given a point P(x, y). It is equidistant from A(3, 6) and B(-3, 4).

So, let's first determine the distance from P to each point. We can use the distance formula:

`d=√((x_2-x_1)^2+(y_2-y_1)^2)`

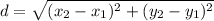
Segment PA:

We will let P(x, y) be (x₂, y₂) and A(3, 6) be (x₁, y₁). By substitution:

`d=\sqrt{(x-3)^2+(y-6)^2`

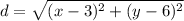
This represents the distance from P to A.

Segment PB:

Again, we will let P(x, y) be (x₂, y₂) and B(-3, 4) be (x₁, y₁). By the distance formula:

`d=√((x-(-3))^2+(y-4)^2)`

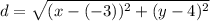
We may simplify:

`d=√((x+3)^2+(y-4)^2)`

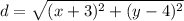
Now, we know that the two distances are equivalent. Hence:

`√((x-3)^2+(y-6)^2)=\sqrt{(x+3)^2+(y-4)^2`

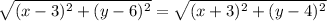
Simplify. Square both sides:

`(x-3)^2+(y-6)^2=(x+3)^2+(y-4)^2`

Square:

`(x^2-6x+9)+(y^2-12x+36)=(x^2+6x+9)+(y^2-8x+16)`

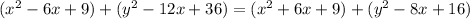
Subtract all terms from the right:

`(x^2-6x+9)-(x^2+6x+9)+(y^2-12x+36)-(y^2-8x+16)=0`

Distribute the negative:

`[(x^2-6x+9)+(-x^2-6x-9)]+[(y^2-12y+36)+(-y^2+8y-16)]=0`

Rearrange:

`[(x^2-x^2)+(-6x-6x)+(9-9)]+[(y^2-y^2)+(-12y+8y)+(36-16)]=0`

Combine like terms;

`(-12x)+(-4y)+(20)=0`

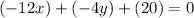
We can divide both sides by -4:

`3x+y-5=0`

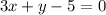
Finally, adding 5 to both sides produces:

`3x+y=5`