Answer:
The angle between the two vectors is 60°
Step-by-step explanation:
Let A and B represent the two vectors, we have;
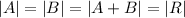
Let
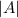 = a,
= a,
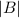 = b, and
= b, and
 = c
= c
We have by cosine rule
c² = a² + b² - 2 × a × b × cos(C)
Where, the angle "C", is the angle between the resultant of the two vectors, a and b and facing the resultant

Given that, a = b = c, we have;
a² = a² + a² - 2 × a × a × cos(C)
a² = 2·a² - 2 × a² × cos(C)
2 × a² × cos(C) = 2·a² - a²
cos(C) = a²/(2·a²) = 1/2
Therefore, angle ∠C = arccosine(1/2) = 60°
The angle between the two vectors = ∠C = 60°.