I need help finding the inverse of this problem

Question

asked Jun 14, 2020 2.5k views

1 Answer

Walid Hanafy · Answer 1 · 2020-06-18T09:29:19+0000

y=√(x-1)+6

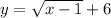
(Notice that we always have
$y\ge6[tex].)</p><p>Swap [tex]x$ and
, then solve for
:

x=√(y-1)+6

x-6=√(y-1)

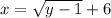
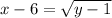
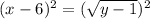
(x-6)^2=(√(y-1))^2

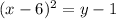
(x-6)^2=y-1

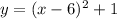y=(x-6)^2+1 (this is the inverse)

###

This inverse is valid only for
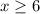$x\ge6$ . Why?

Suppose we take
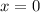x=0 . Then

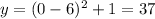
y=(0-6)^2+1=37

This would suggest that in the original equation, we should get
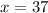x=37 when
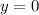y=0 . But when we check this, we end up with

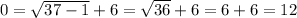
0=√(37-1)+6=√(36)+6=6+6=12

which is clearly not true.