Answer:
21. Option d
22. Option b
23. Option b
Explanation:
The formula to calculate the binomial probability is represented as follows.
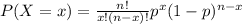
The formula to calculate the binomial probability is represented as follows.
In this formula x represents the number of successes, n represents the number of times the experiment is repeated, p represents the probability of success.
1. First we are asked to calculate the probability of obtaining 3 successes, with n = 6 and p = 0.35.
Then we substitute the values in the formula
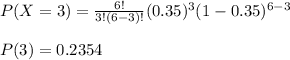
Option d.
2. Second we are asked to calculate the probability of obtaining 5 successes, with n = 20 and p = 60%, p = 0.6.
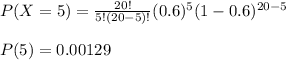
option b
3. Third we are asked to calculate the probability of obtaining 2 successes, with n = 10 and p = 1/2, p = 0.5.
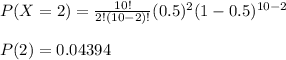
option b