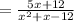Question

Consider the expression below. Place the steps required to determine the sum of the two expressions in the correct order. 3x+6/x^2-x-6 + 2x/x^2+x-12

Answer 1

x-5 edg

Explanation:

Answer 2

1) Factor the denominator and the numerator of each fraction.

2) Simplify.

3) Find the Least common denominator (LCD).

4) Rewrite the LCD. Divide it by the denominator of the first fraction and multiply the result of the division by its numerator (The LCD is the same denominator of the second fraction, so its numerator stays the same).

5) Apply Distributive property on the numerator and on the denominator.

6) Add like terms.

Explanation:

The steps required to determine the sum of the two expressions are:

1) Factor the denominator and the numerator of each fraction:

`(3x+6)/(x^2-x-6)+(2x)/(x^2+x-12)=(3(x+2))/((x-3)(x+2))+(2x)/((x-3)(x+4))`

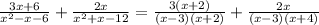
2) Simplify (Remember that
`((x+2))/((x+2))=1`):

`(3)/((x-3))+(2x)/((x-3)(x+4))`

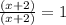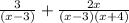
3) Find the Least common denominator (LCD). In this case this is:

`LCD=(x-3)(x+4)`

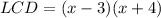
4) Rewrite the LCD. Divide it by the denominator of the first fraction and multiply the result of the division by its numerator. As the LCD is the same denominator of the second fraction, its numerator stays the same:

`=(3(x+4)+2x)/((x-3)(x+4))`

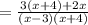
5) Apply Distributive property on the numerator and on the denominator:

`=(3x+12+2x)/(x^2+x-12)`

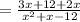
6) Add like terms:

`=(5x+12)/(x^2+x-12)`