Question

I am in need of help

Answer 1

q = 4.9

m∠R = 27.1°

m∠S = 136.9°

Explanation:

To solve the triangle we will use the cosine rule and the sine rule

In the given triangle

∵ q is the opposite side of ∠Q

∵ s is the opposite side of ∠S

∵ r is the opposite side of ∠R

∵ m∠Q = 16°

∵ r = 8 and s = 12

→ By using the cosine rule to find q

∴ q² = r² + s² - 2 r s cos∠Q

→ Substitute the values of r, s, and ∠Q in the rule above

∵ q² = (8)² + (12)² - 2(8)(12)cos(16°)

∴ q² = 23.43775438

→ Take √ for both sides

∴ q = 4.841255455

→ Round it to the nearest tenth

∴ q = 4.9

→ To find angles R and S we will use the sine rule

∵
`(r)/(sin(R))` =
`(q)/(sin(Q))` =
`(s)/(sin(S))`

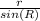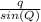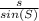
→ Use the first two ratios to find m∠R

∵
`(8)/(sin(R))` =
`(4.841255455)/(sin(16))`

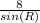→ By using cross multiplication

∴ 4.841255455 × sin(R) = 8 × sin(16)

→ Divide both sides by 4.841255455

∴ sin(R) = 0.4554807874

→ Use
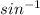`sin^(-1)` to find m∠R

∵ m∠R =
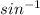`sin^(-1)` (0.4554807874)

∴ m∠R = 27.0958732

→ Round it to the nearest tenth

∴ m∠R = 27.1°

∵ The sum of the measures of the angle in a triangle is 180°

∴ m∠S + m∠Q + m∠R = 180°

→ Substitute the values of m∠Q and m∠R

∵ m∠S + 16° + 27.1° = 180°

∴ m∠S + 43.1 = 180

→ Subtract 43.1 from both sides

∴ m∠S = 136.9°