Question

Which function has a vertex at (2,-9)​

Answer 1

C. f(x) = (x – 5)(x + 1)

Explanation:

Answer 2

The correct option is C) function (x-5)(x+1) has vertex (2,-9).

Explanation:

The vertex of an up down facing parabola of the form y=ax²+bx+c is
`x_v=-(b)/(2a)`

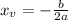
option A) -(x-3)²

Rewrite
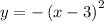`y=-\left(x-3\right)^2` in the form
`y=ax^(2)+bx+c`

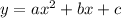
Expand
`-\left(x-3\right)^(2)`

`\left(x^(2)-6x+9\right)`

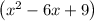
The parabola parameters are: a = - 1, b = 6, c = - 9

`x_v=-(b)/(2a)`

`x_v=-(6)/(2\left(-1\right))`

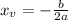
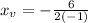
simplify, 3

Plugin
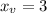`x_v = 3` to find the
`y_v` value

`y_v=-3^(2)+6* 3 -9`

`y_v=-0`

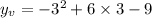
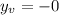
If a<0, then the vertex is a maximum value.

If a>0, then the vertex is a minimum value.

since, a = - 1

Maximum (3,0)

option B) (x+8)²

Rewrite
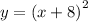`y=\left(x+8\right)^(2)` in the form
`y=ax^(2)+bx+c`

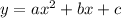
Expand
`\left(x+8\right)^(2)`

`\left(x^(2)+16x+64\right)`

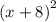
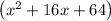
The parabola parameters are: a = 1, b = 16, c = 64

`x_v=-(b)/(2a)`

`x_v=-(16)/(2\left(1\right))`

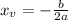
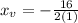
simplify, - 8

Plugin
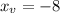`x_v = -8` to find the
`y_v` value

`y_v=-8^(2)+16(-8)+64`

`y_v=-0`

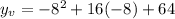
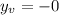
If a<0, then the vertex is a maximum value.

If a>0, then the vertex is a minimum value.

since, a = 1

Minimum (-8,0)

option C) (x-5)(x+1)

Rewrite
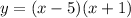`y=(x-5)(x+1)` in the form
`y=ax^(2)+bx+c`

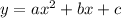
Expand
`y=(x-5)(x+1)`

`\left(x^(2)-4x-5\right)`

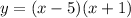
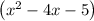
The parabola parameters are: a = 1, b = -4, c = -5

`x_v=-(b)/(2a)`

`x_v=-(-4)/(2\left(1\right))`

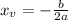
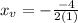
simplify, 2

Plugin
`x_v = 2` to find the
`y_v` value

`y_v=2^(2)-4(2)-5`

`y_v=-9`

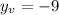
If a<0, then the vertex is a maximum value.

If a>0, then the vertex is a minimum value.

since, a = 1

Minimum (2,-9)

Hence, the correct option is C) function (x-5)(x+1) has vertex (2,-9).