Answer:
+0.231 m/s
Step-by-step explanation:
The problem can be solved by using the law of conservation of momentum. In fact, we have that the total momentum before the collision must be equal to the total momentum after the collision:

where we have
m1 = 245000 kg is the mass of the first car
m2 = 57500 kg is the mass of the second car
u1 = 0.513 m/s is the initial velocity of the first car
u2 = -0.125 m/s is the initial velocity of the second car
v = ? is the final velocity of the two cars together, after the collision
Solving the equation for v, we find
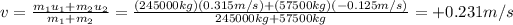
And the direction (positive sign) is the same as the initial direction of the first car.