(a)
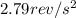
The angular acceleration can be calculated by using the following equation:
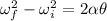
where:
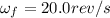 is the final angular speed
is the final angular speed
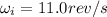 is the initial angular speed
is the initial angular speed
 is the angular acceleration
is the angular acceleration
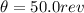 is the number of revolutions made by the disk while accelerating
is the number of revolutions made by the disk while accelerating
Solving the equation for
 , we find
, we find
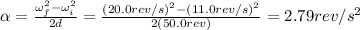
(b) 3.23 s
The time needed to complete the 50.0 revolutions can be found by using the equation:

where
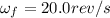 is the final angular speed
is the final angular speed
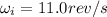 is the initial angular speed
is the initial angular speed
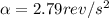 is the angular acceleration
is the angular acceleration
t is the time
Solving for t, we find
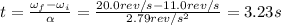
(c) 3.94 s
Assuming the disk always kept the same acceleration, then the time required to reach the 11.0 rev/s angular speed can be found again by using

where
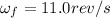 is the final angular speed
is the final angular speed
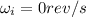 is the initial angular speed
is the initial angular speed
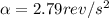 is the angular acceleration
is the angular acceleration
t is the time
Solving for t, we find
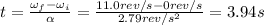
(d) 21.7 revolutions
The number of revolutions made by the disk to reach the 11.0 rev/s angular speed can be found by using
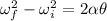
where:
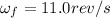 is the final angular speed
is the final angular speed
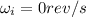 is the initial angular speed
is the initial angular speed
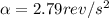 is the angular acceleration
is the angular acceleration
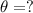 is the number of revolutions made by the disk while accelerating
is the number of revolutions made by the disk while accelerating
Solving the equation for
 , we find
, we find
