1)
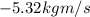
The impulse exerted by the wall on the ball is equal to the change in momentum of the ball:
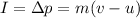
where
m = 0.0950 kg is the mass of the ball
v = -28.0 m/s is the final velocity of the ball (negative because it is away from the wall)
u = +28.0 m/s is the initial velocity of the ball (positive because it is towards the wall)
Substituting into the equation, we find
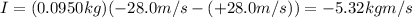
2)
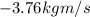
The problem is similar to before, but this time we must consider only the component of the initial and final velocities that are perpendicular to the wall. So we have:
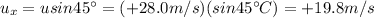 is the component of the initial velocity perpendicular to the wall
is the component of the initial velocity perpendicular to the wall
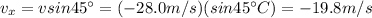 is the component of the final velocity perpendicular to the wall
is the component of the final velocity perpendicular to the wall
Using again the formula for the impulse ,we find
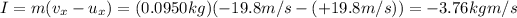
3) -376 N
We know that the impulse is equal to the product between the average force exerted on the ball and the contact time:
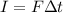
and in this case we have
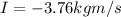 is the impulse
is the impulse
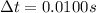 is the contact time
is the contact time
So we can solve the formula for F, and we find

And the negative sign means the direction of the force is away from the wall.