Answer:
The inverse of f(x) is
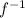 (x) = ±
(x) = ±
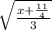 +
+

Explanation:
To find the inverse of the quadratic function f(x) = ax² + bx + c, you should put it in the vertex form f(x) = a(x - h)² + k, where
- h =
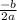
∵ f(x) = 3x² - 3x - 2
→ Compare it with the 1st form above to find a and b
∴ a = 3 and b = -3
→ Use the rule of h to find it
∵ h =
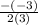 =
=
 =
=

∴ h =

→ Substitute x by the value of h in f to find k
∵ k = 3(
 )² - 3(
)² - 3(
 ) - 2
) - 2
∴ k =

→ Substitute the values of a, h, and k in the vertex form above
∵ f(x) = 3(x -
 )² +
)² +

∴ f(x) = 3(x -
 )² -
)² -

Now let us find the inverse of f(x)
∵ f(x) = y
∴ y = 3(x -
 )² -
)² -

→ Switch x and y
∵ x = 3(y -
 )² -
)² -

→ Add
 to both sides
to both sides
∴ x +
 = 3(y -
= 3(y -
 )²
)²
→ Divide both sides by 3
∵
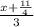 = (y -
= (y -
 )²
)²
→ Take √ for both sides
∴ ±
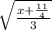 = y -
= y -

→ Add
 to both sides
to both sides
∴ ±
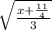 +
+
 = y
= y
→ Replace y by
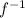 (x)
(x)
∴
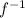 (x) = ±
(x) = ±
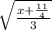 +
+

∴ The inverse of f(x) is
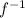 (x) = ±
(x) = ±
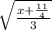 +
+
