Answer:
The answer is (a) ⇒
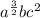
Explanation:
* Lets revise the rational exponent
-
![\sqrt[n]{x^(m)}=x^{(m)/(n)}](https://img.qammunity.org/2020/formulas/mathematics/high-school/jiot6iqkek8asj8b6jxzet1t39wcgmoqon.png)
* So we can change any radical to a rational exponent
* Lets solve our problem
∵
![\sqrt[4]{a^(6)b^(4)c^(8)}](https://img.qammunity.org/2020/formulas/mathematics/high-school/p75m7fq4estupqh4wpw7qyn61gcu43ze5t.png)
* Lets simplify each one
- The first is root 4 of a to the power of 6, we will change the root
and the power to rational exponent 6/4
∴
![\sqrt[4]{a^(6)}=a^{(6)/(4)}](https://img.qammunity.org/2020/formulas/mathematics/high-school/qk2hbv8dunht7pqcts001aqmutd1xvsek3.png) ⇒ simplify the fraction
⇒ simplify the fraction
∴
![\sqrt[4]{a^(6)}=a^{(3)/(2)}](https://img.qammunity.org/2020/formulas/mathematics/high-school/ea4cdtxqydjmw4fx56my4wcm3z4v963dpn.png)
- The second is root 4 of b to the power of 4, we will change
the root and the power to rational exponent 4/4 = 1
∴
![\sqrt[4]{b^(4)}=b^{(4)/(4)}=b^(1)=b](https://img.qammunity.org/2020/formulas/mathematics/high-school/m9qvdv9zzreox92fno5dp7g99xfum5kq5d.png)
- The third is root 4 of c to the power of 8, we will change
the root and the power to rational exponent 8/4 = 2
∴
![\sqrt[4]{c^(8)}=c^{(8)/(4)}=c^(2)](https://img.qammunity.org/2020/formulas/mathematics/high-school/zgyr932pohcu45u8w85hjw70uvfex3ex4h.png)
* The simplest form of
![\sqrt[4]{a^(6)b^(4)c^(8)}=a^{(3)/(2)}bc^(2)](https://img.qammunity.org/2020/formulas/mathematics/high-school/u3nxeuremclomgim7c7vyti8ntyfz5r2me.png)