Question

Simplify the expression (picture provided)

Answer 1

The answer is (a) ⇒
`a^{(3)/(2)}bc^(2)`

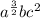
Explanation:

* Lets revise the rational exponent

-
`\sqrt[n]{x^(m)}=x^{(m)/(n)}`

* So we can change any radical to a rational exponent

* Lets solve our problem

∵
`\sqrt[4]{a^(6)b^(4)c^(8)}`

* Lets simplify each one

- The first is root 4 of a to the power of 6, we will change the root

and the power to rational exponent 6/4

∴
`\sqrt[4]{a^(6)}=a^{(6)/(4)}` ⇒ simplify the fraction

∴
`\sqrt[4]{a^(6)}=a^{(3)/(2)}`

- The second is root 4 of b to the power of 4, we will change

the root and the power to rational exponent 4/4 = 1

∴
`\sqrt[4]{b^(4)}=b^{(4)/(4)}=b^(1)=b`

- The third is root 4 of c to the power of 8, we will change

the root and the power to rational exponent 8/4 = 2

∴
`\sqrt[4]{c^(8)}=c^{(8)/(4)}=c^(2)`

* The simplest form of
`\sqrt[4]{a^(6)b^(4)c^(8)}=a^{(3)/(2)}bc^(2)`