Question

A planet has been observed orbiting a nearby star. This star has a mass of 3.5 solar masses, and the planet is 4.2 AU from the star. What is the planet’s orbital period in Earth years? Round your answer to the nearest whole number. __ Earth years

Answer 1

5

Step-by-step explanation:

planet has been observed orbiting a nearby star. This star has a mass of 3.5 solar masses, and the planet is 4.2 AU from the star. What is the planet’s orbital period in Earth years? Round your answer to the nearest whole number.

⇒ 5 Earth yea

Answer 2

4.6 years

Step-by-step explanation:

This is solved using Kepler's third law which says:

`T^2=(4\pi ^2)/(GM) a^2`

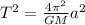
Where

T = Orbital period of the planet (in seconds)

a = Distance from the star (in meters)

G = Gravitational constant

M = Mass of the parent star (in kg)

From the information given

`M = 3.5M_(sun) = 6.96*10^(30) kg`

`a=4.2AU = 6.28*10^(11) meters`

`G = 6.67*10^(-11)m^3kg^(-1)s^(-2)`

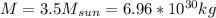
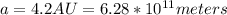
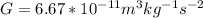
We put this into Kepler's law and get:

`T=\sqrt{(4\pi ^2)/(6.67*10^(-11)*6.96*10^(30)) (6.28*10^(11))^3}=145,128,196 seconds.`

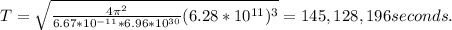
This when converted to years is 4.6 years.