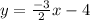Question

Which function is most likely graphed on the coordinate plane below? What is the equation of the line perpendicular to 2x – 3y = 13 that passes through the point (–6, 5)?

Y=2/3 x +9
Y=-3/2x-4
Y=-3/2 x -13
Y=2/3x-1

Answer 1

`y=(-3)/(2)x-4`

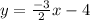
Explanation:

the equation of the line perpendicular to 2x – 3y = 13

It passes through the point (–6, 5)

`2x -3y = 13`

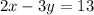
Subtract 2x from both sides

`-3y =-2x+13`

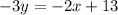
Divide both sides by -3

`y=(2)/(3)x-(13)/(3)`

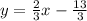
Slope = 2/3

Slope of perpendicular lines are negative reciprocal of one another

slope of perpendicular line is
`(-3)/(2)`

Point (-6,5)

`y-y1=m(x-x1)`

`y-5=(-3)/(2)(x+6)`

`y-5=(-3)/(2)x-9`

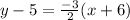
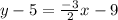
Add 5 on both sides

`y=(-3)/(2)x-4`