Answer:
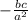
Explanation:
We are given
 ,
,
 and
and
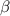 are zeros of the function. We can use the sum and product of roots. You may have come across these equations before ↓
are zeros of the function. We can use the sum and product of roots. You may have come across these equations before ↓


Since the coefficients are already in a, b, and c's, we do not need to sub in anything else.
Now, you are asked to evaluate
 . The next step after finding the roots above ↑, is to factorise this equation to be solved.
. The next step after finding the roots above ↑, is to factorise this equation to be solved.

=
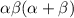
Sub in each respective roots,
=
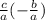
=
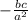
Hope this helped! Ask me if there's any part of the working you don't understand :)