Answer:
a)
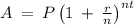
b)
The total amount accrued, principal plus interest, from compound interest on an original principal of $ 4,200.00 at a rate of 3.6% per year compounded 12 times per year over 10 years is $5667.28.
Explanation:
a. Write the function that represents the value of the account at any time, t.
The function that represents the value of the account at any time, t
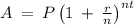
where
P represents the principal amount
r represents Annual Rate
n represents the number of compounding periods per unit t, at the end of each period
t represents the time Involve
b) What will the value be after 10 years?
Given
The principal amount P = $4200
Annual Rate r = 3.6% = 3.6/100 = 0.036
Compounded monthly = n = 12
Time Period = t
To Determine:
The total amount A = ?
Using the formula
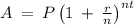
substituting the values
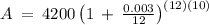

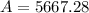 $
$
Therefore, the total amount accrued, principal plus interest, from compound interest on an original principal of $ 4,200.00 at a rate of 3.6% per year compounded 12 times per year over 10 years is $5667.28.