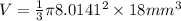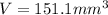Question

Find the volume of each pyramid or come. Round to the nearest tenth if necessary.

Answer 1

QUESTION 1

The given pyramid has a square base.

The volume of this square pyramid is given by;

`V=(1)/(3)* l^2* h`

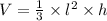
where
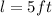`l=5ft` is the length of a side of the square base.

and
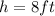`h=8ft` is the height of the pyramid.

We substitute the values into the formula to get;

`V=(1)/(3)* 5^2* 8 ft^3`

`V=66.7 ft^3`

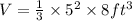
QUESTION 2

The given pyramid has a rectangular base.

The volume of this rectangular pyramid is given by;

`V=(1)/(3)* l* b* h`

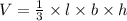
where
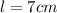`l=7cm` and w=4cm are the length and width of a side of the rectangular base.

and
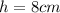`h=8cm` is the height of the pyramid.

We substitute the values into the formula to get;

`V=(1)/(3)* 7* 4* 8cm^3`

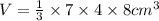
QUESTION 3

The given pyramid has a rectangular base.

The volume of this rectangular pyramid is given by;

`V=(1)/(3)* l* b* h`

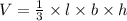
where
`l=10in.` and w=8in are the length and width of a side of the rectangular base respectively.

There is a right triangle created inside this pyramid that can help us find the height of this pyramid.

Notice that the base of this right triangle is half the width of the rectangular base (4in.) and the hypotenuse is 14in.

We need to use Pythagoras Theorem to find the height of this pyramid.

`h^2+4^2=14^2`

`h^2+16=196`

`h^2=196-16`

`h^2=180`

`h=√(180)`

`h=6√(5)in.`

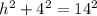
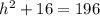
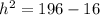
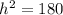
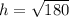
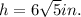
We substitute the values into the formula to get;

`V=(1)/(3)* 10* 8*6√(5)in^3`

`V=160√(5)in^3`

`V=357.8in^3`

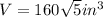
QUESTION 4

The radius of the base of the given cone is 12m.

The height of the cone is 25m.

The volume of a cone is calculated using the formula;

`V=(1)/(3)\pi r^2h`

We substitute the given values to get;

`V=(1)/(3)\pi 12^2* 25m^3`

`V=3769.9m^3`

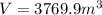
QUESTION 5

The given cone has diameter 14yd.

The radius is half the diameter, r=7yd

The radius(7yd), the height (h), and the slant height(25yd being the hypotenuse) form a right triangle.

We apply the Pythagoras Theorem again to get;

`h^2+7^2=25^2`

`h^2+49=625`

`h^2=625-49`

`h^2=576`

`h=√(576)`

`h=24`

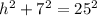
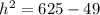
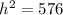
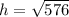
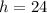
The height of the cone is 24yd.

The volume of a cone is calculated using the formula;

`V=(1)/(3)\pi r^2h`

We substitute the given values to get;

`V=(1)/(3)\pi 7^2* 24yd^3`

`V=1231.5yd^3`

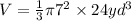
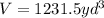
QUESTION 6

The height of the given cone is 18mm.

The radius can be calculated using the tangent ratio.

`\tan(66\degree)=(18)/(r)`

`r=(18)/(\tan(66\degree))`

`r=8.0141yd`

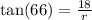
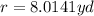
The volume of a cone is calculated using the formula;

`V=(1)/(3)\pi r^2h`

We substitute the given values to obtain;

`V=(1)/(3)\pi 8.0141^2* 18mm^3`

`V=151.1mm^3`