Question

Evaluate 1/x^-2 for x = 7.

Answer 1

49

Explanation:

First we can do x^-2. Anything to a negative power is 1 over that power. 7^-2 is 1/49. Now, we have 1 divided by that. Using the Keep, Flip, Change rule in dividing fractions, we have 1*49. This equals 49. So, your final answer will be 49

Answer 2

For this case we must evaluate the following expression:

`\frac {1} {x ^ {- 2}}\ for\ x = 7`

By definition of power properties we have to:

`x ^ {- 1} = \frac {1} {x ^ 1} = \frac {1} {x}`

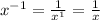
So, rewriting the given expression we have:

`\frac {1} {\frac {1} {x ^ 2}}`

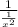
Applying double c we have:

`\frac {1} {\frac {1} {x ^ 2}} = x ^ 2`

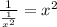
Substituting
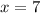`x = 7`we have:

`7 ^ 2 = 49`

Thus, the value of the expression for
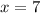`x = 7`is 49

Answer:

49