Hello!
The answer is:
The value of "x" is 10 feet.
Why?
To find the correct answer to this problem, we need to remember the formula to calculate the perimeteer of a rectangle, it's given by the following equation:
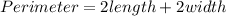
Now, we are given that:
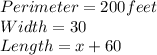
Then, substituting into the equation, we have:

Applying the distributive property, we have:

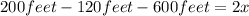
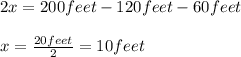
Hence, the length of the gate is 10feet.
Have a nice day!