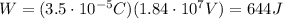What electric potential would be measured at a distance of 12cm from a charge of 3.5 x 10-5 C? What would be the potential if the distance were increased to 30 cm? How much work…

Question

asked Mar 9, 2020 190k views

1 Answer

Tlaminator · Answer 1 · 2020-03-12T21:20:24+0000

1.
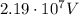
$2.19\cdot 10^7 V$

The electric potential produced by a single point charge is

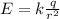
E=k(q)/(r^2)

where

k is the Coulomb's constant

q is the charge

r is the distance from the charge

In this problem,

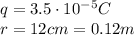
$q=3.5\cdot 10^(-5) C\\r=12 cm=0.12 m$

so the electric potential is

$E=(9\cdot 10^9 Nm^2 C^(-2))((3.5\cdot 10^(-5) C))/((0.12 m)^2)=2.19\cdot 10^7 V$

2.
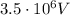
$3.5\cdot 10^6 V$

Applying the same formula used before

The electric potential produced by a single point charge is

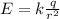
E=k(q)/(r^2)

where in this case we have

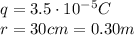
$q=3.5\cdot 10^(-5) C\\r=30 cm=0.30 m$

the electric potential is

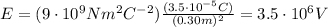
$E=(9\cdot 10^9 Nm^2 C^(-2))((3.5\cdot 10^(-5) C))/((0.30 m)^2)=3.5\cdot 10^6 V$

3. 644 J

The work done to carry a charge q through a potential difference of
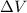$\Delta V$ is given by

$W=q\Delta V$

In this problem, we have

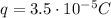$q=3.5\cdot 10^(-5)C$ is the charge

$\Delta V=V(12 cm)-V(30 cm)=2.19\cdot 10^7 V-3.5\cdot 10^6 V=1.84\cdot 10^7 V$ is the potential difference

Therefore, the work done is

$W=(3.5\cdot 10^(-5) C)(1.84\cdot 10^7 V)=644 J$