Hello!
The answer is:
The lengths of the diagonals are:
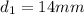
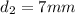
Why?
To solve the problem, we need to use the formula to calculate the area of a rhombus involving its diagonals and create a relation between the diagonals of the given rhombus.
So, from the statement we know that:

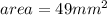
We need to use the following formula
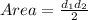
Then,
Substituting and calculating we have:
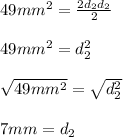
We have that:
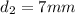
So, calculating the length of the diagonal 1, we have:

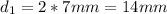
Hence, we have that the answers are:
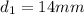
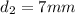
Have a nice day!