Answer: m∠F=67°
Explanation:
Given the right triangle FHG and the lengths of all its sides:
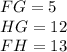
You can calculate the measure of the angle identified as m∠F with:
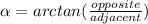
Where the opposite side is 12, the adjacent side is 5 and the angle
 is m∠F.
is m∠F.
Then, substituting values into
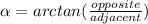 :
:

To the nearest degree:
m∠F=67°