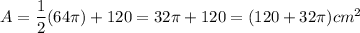Question

Can you help me please

Answer 1

`\large\boxed{A=(120+32\pi)cm^2}`

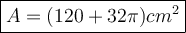
Explanation:

Look at the picture.

We have the half of circle and a triangle.

The fromula of an area of a circle:

`A_O=\pi r^2`

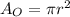
r - radius

We have r = 8cm. Substitute:

`A_O=\pi(8)^2=64\pi\ cm^2`

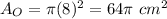
The formula of an area of a triangle:

`A_\triangle=(bh)/(2)`

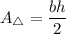
b- base

h - height

We have b = 8cm + 8cm = 16cm and h = 15cm. Substitute:

`A_\triangle=((16)(15))/(2)=(8)(15)=120\ cm^2`

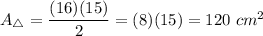
The area of the figure:

`A=(1)/(2)A_O+A_\triangle`

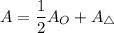
Substitute:

`A=(1)/(2)(64\pi)+120=32\pi+120=(120+32\pi)cm^2`