Answer:
The transformation of f(x) on a coordinate plane relative to g(x) is that the graph of g(x) has been shifted three units to the right and two units upward.
Explanation:

By knowing this, we can see that the function
 takes the following form:
takes the following form:
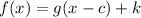
Therefore, we can say that
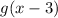 represents shifting the graph three units to the right and ultimately
represents shifting the graph three units to the right and ultimately
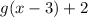 tells us that the graph is shifted two units upward. Finally:
tells us that the graph is shifted two units upward. Finally:
- The transformation of f(x) on a coordinate plane relative to g(x) is that the graph of g(x) has been shifted three units to the right and two units upward.