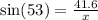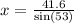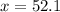Question

Please Help! Math help Needed

Answer 1

The exact value is 24√3

The approximate value is 41.6 to the nearest tenth.

x=52.1 units.

Step-by-step explanation

Let the blue dotted line be h units.

This line is opposite to the 60° angle.

The side length of the triangle which is 24 units is adjacent to the 60° angle.

So we use the tangent ratio,

`\tan(60 \degree) = (opposite)/(adjacent)`

`\tan(60 \degree) = (h)/(24)`

`√(3) = (h)/(24)`

`h = 24 √(3)`

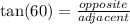
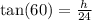
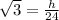
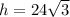
This is the exact value.

`h = 41.6`

This is that approximate value to the nearest tenth.

To find the side length , x, we need to use the second triangle.

`\sin(53\degree) = (h)/(x)`

`\sin(53\degree) = (41.6)/(x)`

`x = (41.6)/(\sin(53\degree))`

`x = 52.1`