Answer:
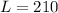 ,
,
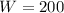
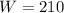 ,
,
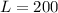
Explanation:
By definition, the perimeter of a rectangle is:

Where:
P is the perimeter, L is the length and W is the width
Also, the area of a rectangle is:
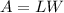
Where L is the length of the base and W is the width.
We know that for this rectangle:

Now we have two equations and two unknowns (L and W)
Then we solve the system.
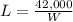
Now we substitute this relation in the perimeter equation.
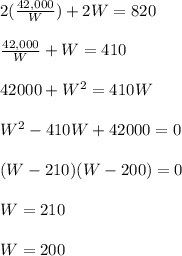
Then for W=210:

And for W=200
