Question

Rounded to the nearest hundredth, what is the positive solution to the quadratic equation 0 = 2x2 + 3x – 8? Quadratic formula: x =

Answer 1

1.39

Step-by-step explanation

The given quadratic equation is

`0 = 2 {x}^(2) + 3x - 8`

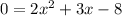
This is the same as,

`2 {x}^(2) + 3x - 8 = 0`

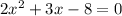
Comparing to

`a {x}^(2) + bx + c = 0`

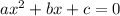
We have

a=2, b=3,c=-8

Using the quadratic formula, the solution is given by:

`x = \frac{ - b \pm \: \sqrt{ {b}^(2) - 4ac} }{2a}`

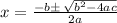
We substitute the values to get,

`x = \frac{ - 3\pm \: \sqrt{ {3}^(2) - 4(2)( - 8)} }{2(2)}`

`x = ( - 3\pm \: √( 73) )/(4)`

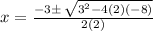
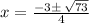
The positive root is

`x = ( - 3 + \: √( 73) )/(4) = 1.39`

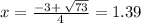
to the nearest hundredth.