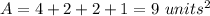Question

Which of the following shows that the two composite figures cover the same area? HELP ASAP!!

Answer 1

For both figures
`A=4+2+2+1=9\ units^(2)`

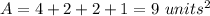
Explanation:

we know that

The area for both composite figures is equal to the area of a square plus the area of two isosceles right triangles plus the area of a smaller isosceles triangle

so

Area of the square

`A=2^(2)=4\ units^(2)`

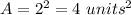
Area of the isosceles right triangle

`A=(1/2)(2)(2)=2\ units^(2)`

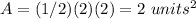
Area of the smaller isosceles triangle

`A=(1/2)(2)(1)=1\ units^(2)`

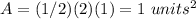
The area of the composite figure is

`A=4+2+2+1=9\ units^(2)`