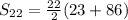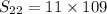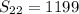Question

Is the sum the sum of the arithmetic 1635?​

Answer 1

1199

Explanation:

There are 22 terms in the sum:

23 + 26 + 29 + ... + 80 + 83 + 86 =

= (23 + 86) + (26 + 83) + ... + (53 + 56)

= 109 + 109 + ... + 109

= 11(109)

= 1199

Answer 2

ANSWER

1199

EXPLANATION

The given series is


`\sum_(n=9)^(30)(3n-4)`

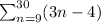
To find the first term of this series, we put n=9 into the formula.


`a = 3(9) - 4 = 23`

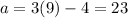
To find the last term, we put n=30


`l = 3(30) - 4 = 86`

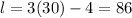
There are 22 terms from the 9th term to the 30th term

The sum of the consecutive n-terms of an arithmetic series is given by;


`S_n= (n)/(2) (a + l)`

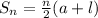
We substitute n=22, a=23, and l=86 to get;


`S_ {22}= (22)/(2) (23 + 86)`


`S_ {22}= 11 * 109`


`S_ {22}= 1199`