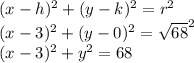Answer:
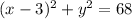
Explanation:
The vertex form of the equation of a circle is
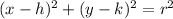 where (h,k) is the center of the circle and r is the radius. This circle has center (3,0). Find the radius using the distance formula with (3,0) and (1,8).
where (h,k) is the center of the circle and r is the radius. This circle has center (3,0). Find the radius using the distance formula with (3,0) and (1,8).
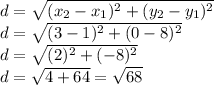
Substitute h = 3, k = 0 and r = √68 into the vertex form. Then simplify for the equation.